Definition: A minimum variance portfolio indicates a well-diversified portfolio that consists of individually risky assets, which are hedged when traded together, resulting in the lowest possible risk for the rate of expected return.
What Does Minimum Variance Portfolio Mean?
What is the definition of minimum variance portfolio? This leverages the risk of each individual asset with an offsetting investment, thus hedging the total portfolio risk for the level of risk accepted with respect to the expected rate of portfolio return.
Put simply each investment in a minimum variance portfolio is risky if traded individually, but when traded in the portfolio the risk is hedged. The term originates from the Markowitz Portfolio Theory, which suggests that volatility can be used to replace risk and, therefore, less volatility variance correlates with less investment risk.
Let’s look at an example.
Example
Andrew is a financial analyst, and he works at an advisory firm. His manager asked Andrew to calculate the minimum variance portfolio for several risky stocks held by the company’s most prominent customer.
The portfolio invests in five stocks with an allocation of 15%, 20%, 12%, 36%, and 17%. Andrew calculates the standard deviation using the STDEV function in Excel and the annual return of each stock using the average return as follows:
Annual return stock A = (1+ Average return)t-1 = (1+1.68%)12-1 = 22.19% and so on for the rest of stocks.

Then, Alex calculates the correlation and covariance of stocks contained in the portfolio to construct an optimized portfolio that can minimize the risk. He applies the correlation matrix in Excel to investigate the dependence between the stock returns, and he calculates the covariance using the VARP function in Excel to find the mean value of the returns for each stock as follows:
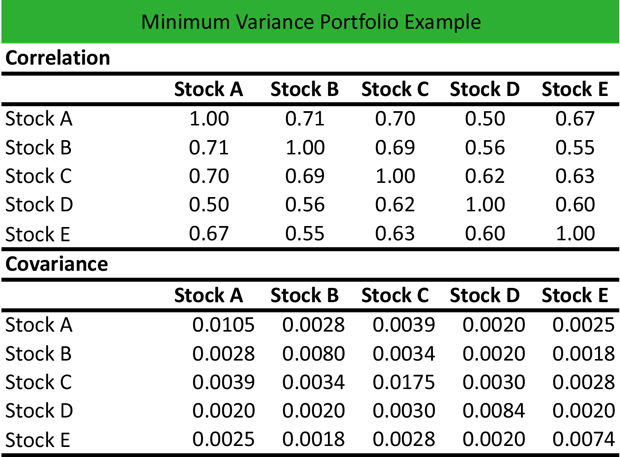
Then, he uses the weight of each stock and the covariance to construct the optimized portfolio. The total of weights is equal to 1 (100%).
The optimization is derived as follows:
- Stock A: 0.15 x 0.0105 x 0.15 = 0.0002
- Stock B: 0.20 x 0.0028 x 0.20 = 0.0001
- Stock C: 0.12 x 0.0039 x 0.12 = 0.0001
- Stock D: 0.36 x 0.0020 x 0.36 = 0.0001
- Stock E: 0.17 x 0.0025 x 0.17 = 0.0001
The same formula applies for each weight, thus deriving the total optimized returns for each stock, as follows:
Andrew calculates the portfolio variance by adding the individual values of each stocks:
Portfolio variance = 0.0006 + 0.0007 + 0.0006 + 0.0016 + 0.0005 = 0.0040 = 0.40%
Then, he calculates the portfolio standard deviation:
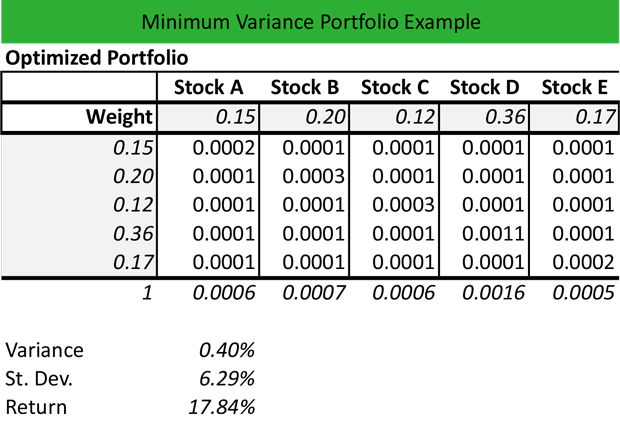
Portfolio standard deviation = Portfolio variance0.5 = 0.00400.5 = 0.0629 = 6.29%
Finally, he calculates the optimized portfolio return using the weight of each stock multiplied by the annual return of the stock, as follows:
Optimized portfolio return = 0.15 x 22.19% + 0.20 x (-9.25%) + 0.12 x 56.72% + 0.36 x 13.27% + .017 x 28.11% = 3.33% -1.85% + 6.81% + 4.78% + 4.78% = 17.84%
Summary Definition
Define Minimum Variance Portfolio: MVP means a diversified portfolio that mitigates risk properly.