Definition: The objective function is a mathematical equation that describes the production output target that corresponds to the maximization of profits with respect to production. It then uses the correlation of variables to determine the value of the final outcome. In other words, it’s a formula businesses use to achieve profitability and production goals.
What Does Objective Function Mean?
An objective function attempts to maximize profits or minimize losses based on a set of constraints and the relationship between one or more decision variables. The constraints could refer to capacity, availability, resources, technology, etc. and reflect the limitations of the environment in which the business operates. Each combination of values that apply to decision variables forms the solution of the business problem. When these values satisfy the constraints of the problem, the solution is the feasible solution.
The objective function can take the form of z = f (xi)
Let’s look at an example.
Example
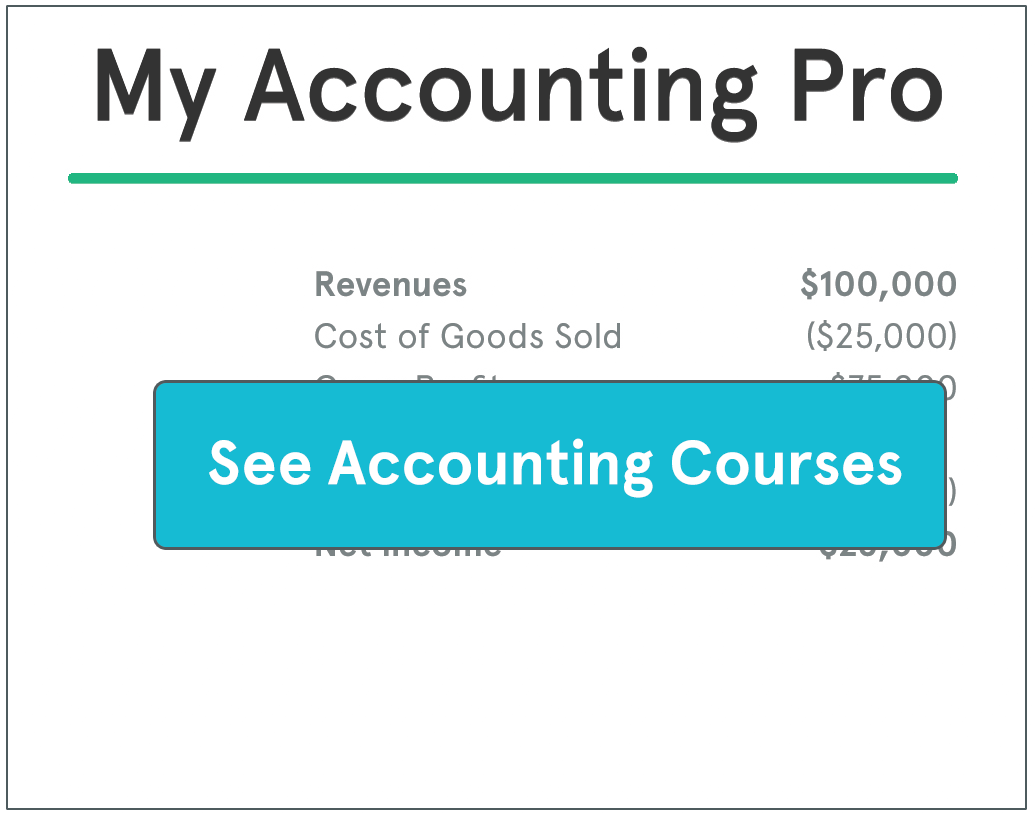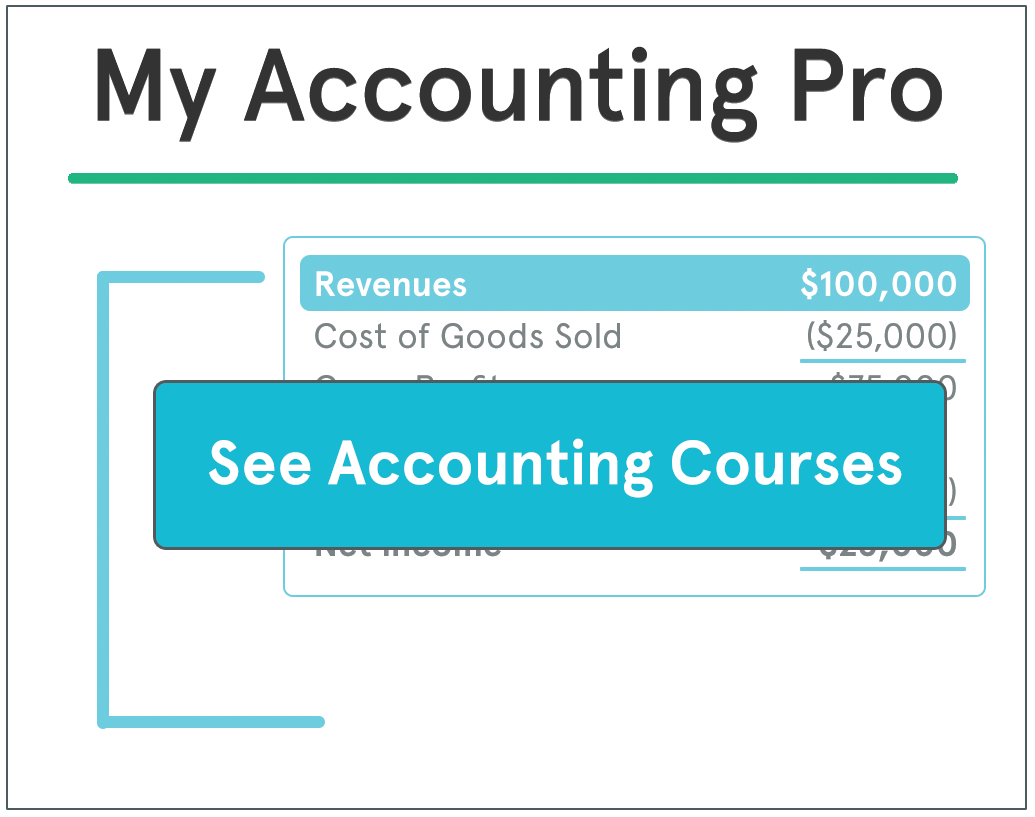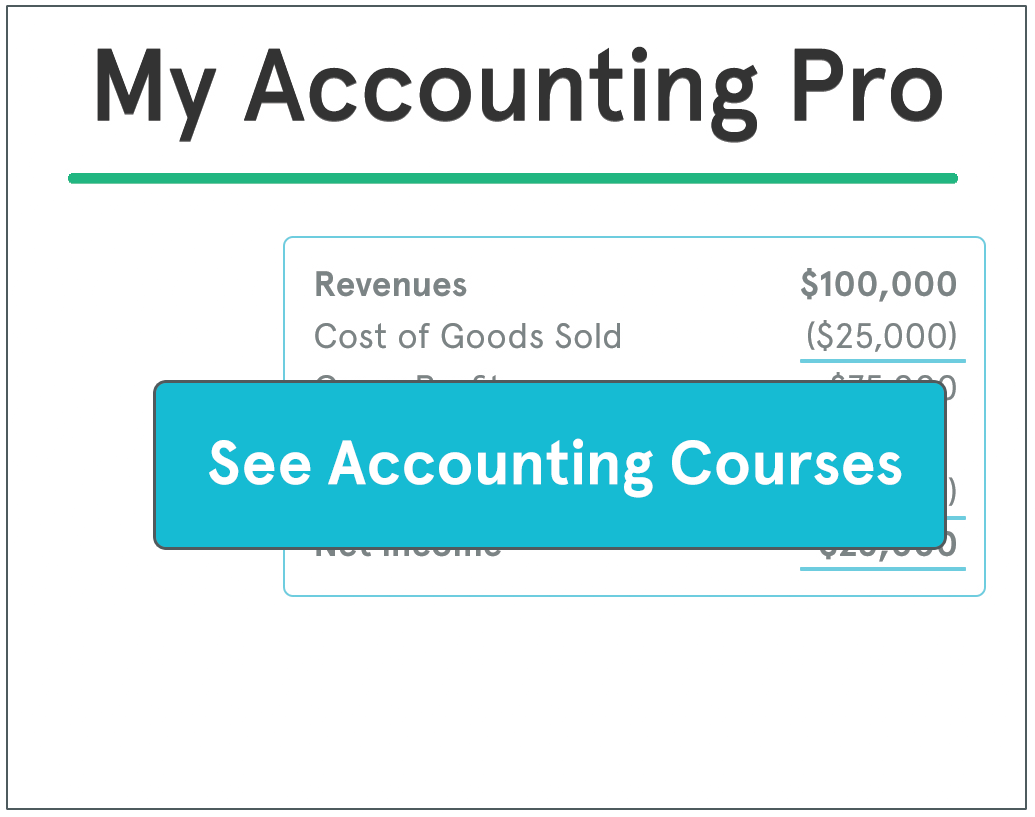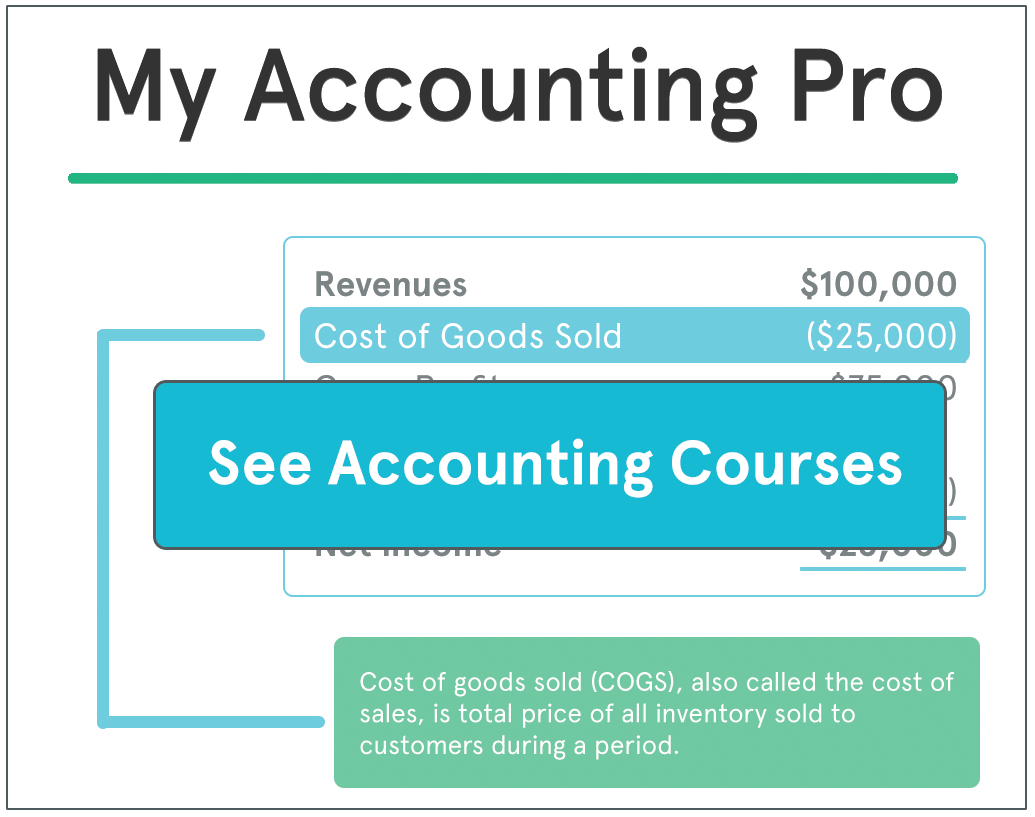
A factory produces building materials. Sale price:
Product A = $140 / ton, Product B = $160 / ton.
During construction, a special ingredient X is added. Each ton of product A produced requires 2 cubic meters of ingredient X and each ton of product B requires 4 cubic meters of ingredient X. Only 28 cubic meters of ingredient X are available in production per week. The worker who produces the materials can work up to 50 hours / week. The machine producing the materials is able to construct a ton of product at a time, while the process lasts 5 hours. The finished products are stored in bins: 8 tons of product A and 6 tons of product B.
The purpose of solving the problem is to determine the quantity of product A and of product B that can be produced every week in order to achieve maximization of the total weekly profit.
Satisfaction production conditions:
- Total weekly profit: (z) = 140) = 140×1 + 160×2 (where x1= product A and x2= product B)
- Ingredient Availability X: 2×1 + 4×2 ≤ 28
- Total Production time: 5×1 + 5×2 ≤ 50
- Produced product A per week: ≤ 8 tons
- Produced product B per week: ≤ 6 tons
Possible Solution: Should satisfy all the constraints simultaneously.
Optimal Solution: further than satisfying all the constraints simultaneously, it should provide the maximum value of the objective function = total weekly profit
A negative output of a product is not possible, therefore variables x1 and x2 must be positive.