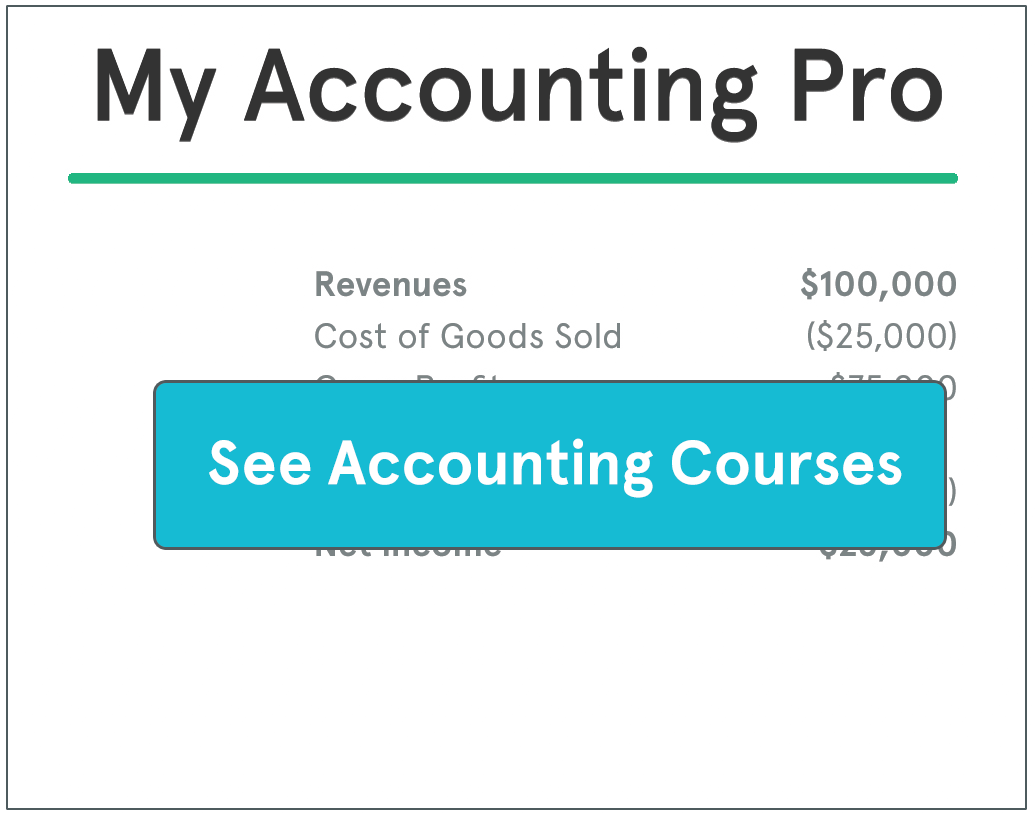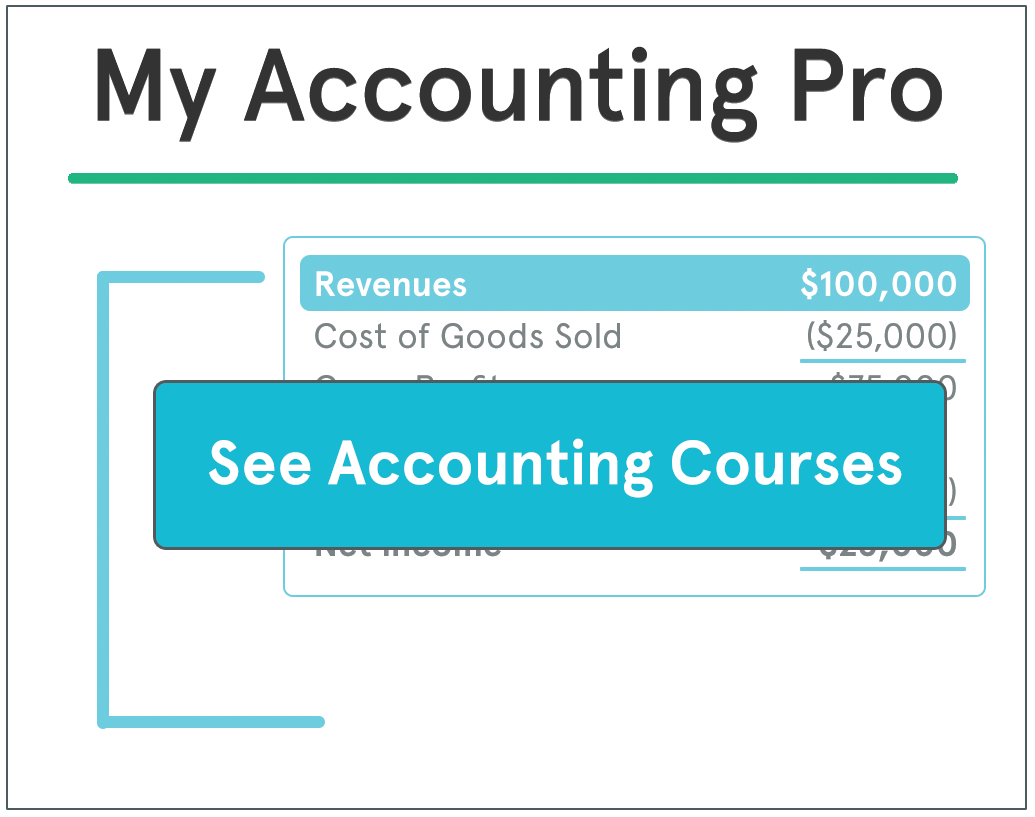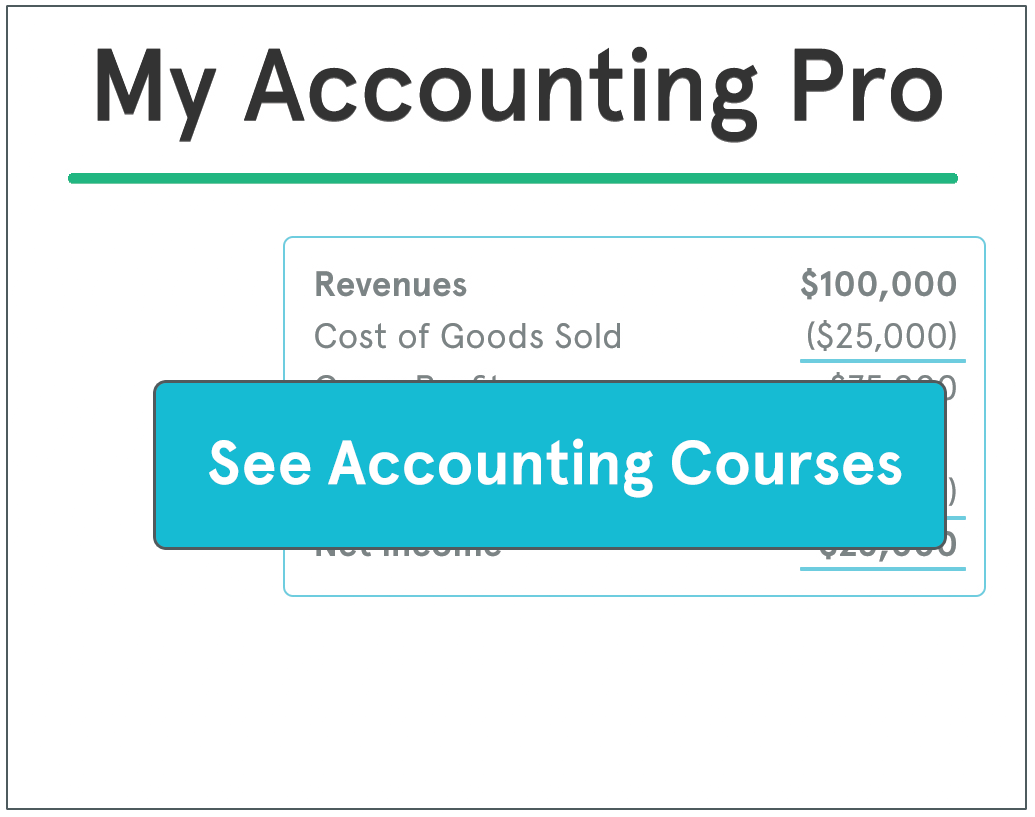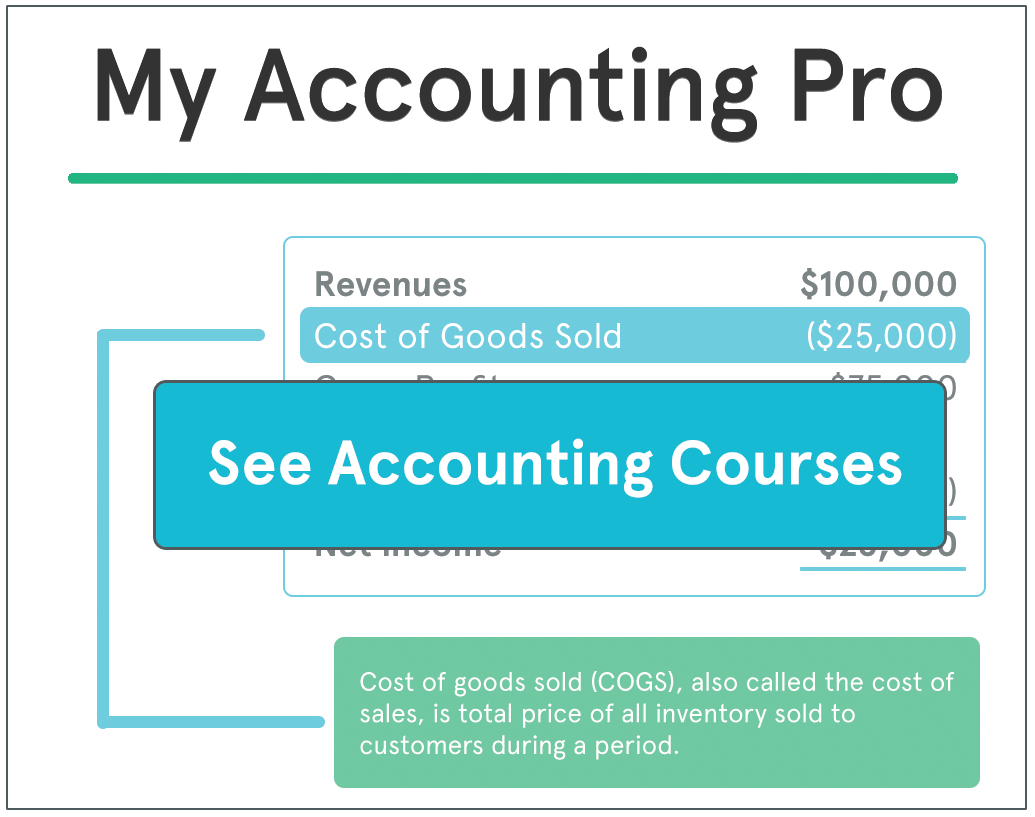
Definition: Zero sum game is a situation in economics where one party’s win causes other parties to lose exactly in the same proportion. The aggregate result of all parties results equals zero.
What Does Zero Sum Game Mean?
Zero-Sum Games are described by Game Theory, a field of economics that study the interaction between participants inside the “game”, a term that describe a given economic scenario. This theory was developed by John von Neumann in its book “Theory of Games and Economic Behavior”. Mathematical models are used to describe the possible outcomes of strategic decisions. One of these “games” are zero-sum games.
These are situations where no value is created, which means that if one of the parties win the other party loses exactly the same amount won by the other side, therefore, the overall result of combining both transactions is zero. This is the case for penny flipping. If two parties bet $1 in a coin flipping game and one party picks heads while the other picks tails, the game is a zero-sum game. The result of the coin flip will add $1 to one of the parties while the other one will lose $1 as a result.
Example
Three friends met a Saturday night to play poker. The host conveyed them to bet a minimum of $100 each with the possibility to add $100 more to the table if at some point any of them wanted to refill their chips. A poker game involves betting, which is a zero-sum game.
The first round begun and Friend #1 decided to bet $6 while Friend #2 and #3 decided to go along and match his bet. After the flush was shown, before they had to show their cards, Friend #2 raised his bet to $15. Friend #1 folded but Friend #3 called the bet. Cards were shown and Friend #2 won. The zero-sum game was the following: Friend #2 got a total of $15 (Friend #3) plus $6 (Friend #1), which means he won a total of $21 as a result. On the other hand the combined losses of Friend #3 and #1 were also $21.